![[Stan] Pystanで始めるガウス線形単回帰](https://devio2023-media.developers.io/wp-content/uploads/2016/06/stan_eyecatch.png)
[Stan] Pystanで始めるガウス線形単回帰
この記事は公開されてから1年以上経過しています。情報が古い可能性がありますので、ご注意ください。
はじめに
Stanは統計的なモデリングのためのDSLです。社会学や生物学、物理、工学と至る分野のデータ分析及び予測に用いられています。今回はStanを用いるための始めの一歩としてPythonのインターフェイスであるpystanとインタラクティブなコード実行環境であるjupyter notebookを用いてモデルを作成してみました。モデルとしては手頃な題材であるガウス分布の線形回帰モデルを用いました。
Stan
多くの機械学習ライブラリでは教師付き機械学習に関して、手法ごとのモデルに応じてインターフェイスが提供されていますが、Stanはそのモデルを作成するDSLとなっているため、ライブラリの枠にとどまらない柔軟な手法を試すことができます。
パラメータを算出する手法としてはMCMC(マルコフ連鎖モンテカルロ法)の改善版であるHMC(ハミルトニアンモンテカルロ法)を用いています。(本記事ではMCMC,HMCについて深く突っ込まずにチュートリアル的にStanを動かしていきます)
線形単回帰モデル
線形単回帰モデルは以下のような一つの説明変数 \( X \)に傾き \( \beta \) と切片 \( \alpha \) を合わせたものが目的変数 \( Y \) を記述するというモデルです
[latex] Y = \alpha + \beta X + \epsilon [/latex]
ここで \( \epsilon \) については平均0, 分散 \( \sigma \) のガウス分布 \( N \) に従います
[latex] \epsilon \sim N(0, \sigma) [/latex]
これらの関係を一つにまとめると
[latex] Y \sim N(\alpha + \beta X, \sigma) [/latex]
のように記述できます。
サンプル・データセット
今回はサンプル・データとしてRのデータ・セットの中で線形回帰を適用できそうな米国女性の平均身長と平均体重のデータ・セットを用います。
このデータ・セットを教師データとして訓練した線形単回帰モデルを用いることで体重を入力として身長を予測することがある程度できるようになります。
このサンプルデータセットを題材にして、それを分析するための環境のセットアップから行っていきます。
環境準備
MacOSX 10.10.5 上で動作確認しました。
pyenvのインストール
brewを用いてpythonの実行環境を管理できるpyenvをインストールします。
$ brew install pyenv
.bshrc, .zshrc等のシェル設定ファイルに下記設定を追記します。
export PYENV_ROOT="$HOME/.pyenv" export PATH="$PYENV_ROOT/bin:$PATH" eval "$(pyenv init -)"
anacondaのインストール
いまインストールしたpyenvを用いてデータ分析のための環境であるanaconda-4.0.0をインストールします。
$ pyenv install anaconda-4.0.0 $ pyenv local anaconda-4.0.0
pystanのインストール
anaconda-4.0.0環境にはpystanが標準でインストールされていないため、現在の環境のpythonパッケージマネージャpip経由でインストールをします。
$ pip install pystan
jupyter notebookの起動
インストールが完了したら、下記コマンドでanaconda環境にインストールされているjupyter notebookを起動します
$ jupyter notebook
学習データの配置
jupyter notebookの実行ディレクトリ上に以下のtsvファイルを展開します。
women.tsv
id height weight 1 58 115 2 59 117 3 60 120 4 61 123 5 62 126 6 63 129 7 64 132 8 65 135 9 66 139 10 67 142 11 68 146 12 69 150 13 70 154 14 71 159 15 72 164
Stanをもちいた線形単回帰モデルの作成
線形単回帰モデルは下記のような形をしていました
[latex] Y \sim N(\alpha + \beta X, \sigma) [/latex]
これに対応するStanのコードは次のようになります
data { // 学習のためのデータを宣言するdataセクション
int<lower=0> N; // 学習データの数
vector[N] x; // 単回帰モデルの入力xに対応するデータ配列
vector[N] y; // 単回帰モデルの出力yに対応するデータ配列
}
parameters { // モデル構築のためのパラメータを宣言するparameterセクション
real alpha; // 単回帰モデルの切片
real beta; // 単回帰モデルのxに掛かる係数
real<lower=0> sigma; // 単回帰モデルからの散らばり具合を表す分散のルート
}
model { // モデルを宣言するmodelセクション
y ~ normal(alpha + beta * x, sigma); // 線形単回帰モデル
}
- dataセクション 外部から受け取る学習データの内容を宣言する部分です。本記事では体重と身長の対応を集めたサンプルデータセットの形式に相当します。
- paramterersセクション モデルで用いるパラメータの宣言を行う部分です。実数、非負などといったパラメーターの性質を指定できます。本記事では線形単回帰モデルの切片や係数、分散に相当します。
- modelセクション 実際に用いられるモデルの宣言を行う部分です。数式に対応したモデルをこの部分で構築します。本記事では線形単回帰モデルに相当します。
他にもStanでは transformed dataセクション や transformed parametersセクション があります。こちらはその名の通り入力データやパラメータの一時変数への受け渡しを行える部分です。
pystanでのモデル構築
jupyter notebook上で上記Stanモデルをpystanを用いてインポートします。
下記にnotebook上で実行するコードを貼りだしていきそのコードでなにが行われているかについて見ていきます。jupyter notebook上のサンプルコードはこちらにもアップしてあります
In [1]:
import pystan import numpy as np %matplotlib inline
pystanパッケージとnumpyパッケージをインポートします。三行目は図表出力のためのmatplotlibパッケージで表示される図をjupyter notebookにインライン表示するためのコードです。
In [2]:
model = """
data {
int<lower=0> N;
vector[N] x;
vector[N] y;
}
parameters {
real alpha;
real beta;
real<lower=0> sigma;
}
model {
y ~ normal(alpha + beta * x, sigma);
}
"""
model変数に先ほどのStanコードを代入します。後でpystanパッケージのstan関数を用いてこのモデルを用いたパラメータ予測を行います。
In [3]:
datum = np.loadtxt("women.tsv", delimiter="\t", usecols=(1, 2), skiprows=1)
weights = np.transpose(datum)[0]
heights = np.transpose(datum)[1]
一行目はdatum変数に学習データの内容を展開しています。tsv形式のファイルに関してはnumpyの loadtxt 関数でdelimiter をタブ文字に指定することでインポートできます。インポートしたい列の指定を usecols で行い、はじめにスキップする行数を skiprows で指定できます。
二、三行目では展開された学習データをもとに、体重、身長の配列を作成しています。transposeしているのはもともとのデータが下記のように列の項目として体重と身長を有するためです。
In [4]:
datum
Out [4]:
array([[ 58., 115.],
[ 59., 117.],
[ 60., 120.],
[ 61., 123.],
[ 62., 126.],
[ 63., 129.],
[ 64., 132.],
[ 65., 135.],
[ 66., 139.],
[ 67., 142.],
[ 68., 146.],
[ 69., 150.],
[ 70., 154.],
[ 71., 159.],
[ 72., 164.]])
In [5]:
fit = pystan.stan(model_code=model, data=dict(y=heights, x=weights, N=len(heights)))
stan関数を用いてStanで作成したモデルによるパラメータの推測を行い、その結果をfit変数に展開しています。
この計算の実行にはしばらく時間がかかりますが、jupyter notebookを実行しているシェル上に以下のような出力がなされれば完了です。
Chain 1, Iteration: 2000 / 2000 [100%] (Sampling)# # Elapsed Time: 0.273571 seconds (Warm-up) # 0.251955 seconds (Sampling) # 0.525526 seconds (Total) # Chain 2, Iteration: 2000 / 2000 [100%] (Sampling)# # Elapsed Time: 0.325311 seconds (Warm-up) # 0.192349 seconds (Sampling) # 0.51766 seconds (Total) #
これはHMCによるパラメータ予測が完了したことを表しています。
In [6]:
fit
Out [6]:
Inference for Stan model: anon_model_d5c9515652e6c049f3e6b6cc53cb45ed.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
alpha -87.32 0.28 6.57 -100.2 -91.55 -87.45 -83.19 -74.06 554.0 1.0
beta 3.45 4.3e-3 0.1 3.24 3.38 3.45 3.51 3.65 554.0 1.0
sigma 1.69 0.01 0.38 1.13 1.42 1.62 1.89 2.6 640.0 1.01
lp__ -14.01 0.05 1.26 -17.22 -14.64 -13.7 -13.06 -12.52 552.0 1.0
Samples were drawn using NUTS(diag_e) at Mon Jun 27 11:33:12 2016.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
これはモデル予測の結果です。途中の表のようになっている部分が各パラメータに関するベイズ推定による最終的に収束した事後分布の統計量になっています。
特にここでは深追いしませんが、mean(平均)の列における各パラメータの値がモデルによってはじき出されたパラメータの代表値として考えられるとして進めます。
In [7]:
fit.plot()
以下のような図が出力として表示されます。
Out [7]:
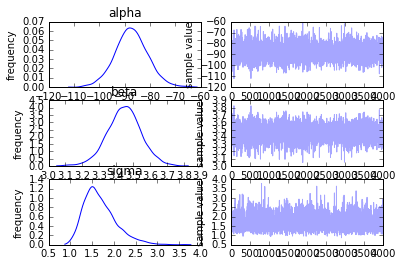
このグラフは各種パラメータの最終的な事後分布(左側)と各種パラメータのベイズ推定のイテレーション回数を横軸とした推移図(右側)です。初期の分布から余り予測値は推移していないことが分かりますが、単に予測しやすいデータ・セットを用いているためで、実際のデータや単回帰モデル以外のモデルを用いるとまたこのグラフは変わってくるかと思います。
In [8]:
import matplotlib.pyplot as plt
matplotlibのプロットを行うpyplotモジュールをpltとしてインポートします。
In [9]:
samples = fit.extract(permuted=True) alpha = np.mean(samples["alpha"]) beta = np.mean(samples["beta"])
先ほどのパラメータ算出の過程はfit変数の中に全て入っていますが、それを抽出するために extract 関数を用います。permuted に True を指定することでパラメータ算出の過程の結果が以下のような辞書形式でまとめられます。
In [10]:
samples
Out [10]:
OrderedDict([(u'alpha',
array([ -85.17751526, -89.09972412, -96.56231134, ..., -77.48670801,
-97.5094758 , -100.19309052])),
(u'beta',
array([ 3.41249023, 3.47840149, 3.58665085, ..., 3.29621573,
3.60254252, 3.63828803])),
(u'sigma',
array([ 1.94685732, 1.51147492, 1.17916977, ..., 1.31154517,
2.03663507, 1.86467662])),
(u'lp__',
array([-13.38668679, -12.67667206, -15.20328873, ..., -14.51470653,
-14.3988749 , -14.91153716]))])
In [11]:
plt.plot(weights, heights, "o") plt.plot(weights, alpha + beta * weights) plt.show()
モデルを用いたベイズ推定ではじき出されたパラメータを元に算出した \( \alpha, \beta \) をもとに作成した直線ともとのデータをプロットしています。このコードを実行すると下記のような図が出力されます。
Out [11]:
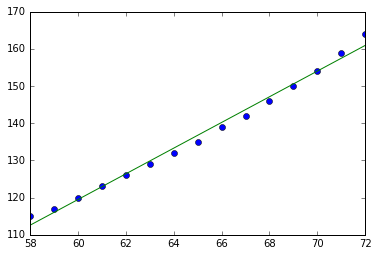
データ・セットに線形モデルがFitしている様子が伺えます。
線形単回帰モデルに絡んだ手法
重回帰
単回帰は入力が単一の説明変数でしたが、説明変数が複数のときは下記のように表せ
[latex] Y = \beta_0 + \sum^p_{i = 1} \beta_i X_i + \epsilon [/latex]
このモデルは重回帰とよばれます。
さらに出力がベクトルであるとき、 \( Y, \beta, \epsilon \) をベクトル、\( X_i \) については定数項を中に入れ込んで行列 \( X \) とすることで下記のような一般線形モデルの表記になります
[latex] \boldsymbol{Y} = X \boldsymbol{\beta} + \boldsymbol{\epsilon} [/latex]
一般化線形モデル
上記の \( \epsilon \) がガウス分布 \( N \) のみならず一般的な確率分布(厳密には指数分布族)に従うものを一般化線形モデルと呼びます。
まとめ
本記事では線形単回帰モデルを題材としてPythonとStanを用いた分析のチュートリアルを行いました。この記事をもとにしてStanで用いられているHMC、MCMCの手法や、より発展的なモデルの解説記事等を今後執筆できればと思っています。







